Análisis Exploratorio de Datos: Desentrañando la Verdad de tus Datos

Por Maicel Monzon

Introducción

El Análisis Exploratorio de Datos (EDA), introducido y formalizado por John Tukey, no es un conjunto de gráficos decorativos ni un trámite previo al modelado. Es una fase de razonamiento empírico cuyo objetivo principal es comprender qué tipo de datos tenemos realmente entre manos antes de imponerles una estructura estadística o algorítmica.

Hablar de EDA como una “filosofía” no implica vaguedad, sino todo lo contrario: implica aceptar que los datos deben examinarse, interrogarse y ponerse a prueba antes de asumir supuestos. En la práctica, el EDA permite:

• entender la estructura del conjunto de datos,
• detectar problemas de calidad,
• identificar patrones plausibles,
• y reconocer anomalías que requieren explicación, no ocultamiento.

Un principio recurrente en ciencia de datos es GIGO (Garbage In, Garbage Out). Aunque suele formularse de manera tajante, conviene interpretarlo con cuidado: no toda imperfección invalida un análisis, pero los problemas no detectados sí lo hacen. El EDA no garantiza datos “perfectos”, pero sí datos conocidos, y esa diferencia es crítica.

Un Flujo de Trabajo Práctico de EDA

El EDA no es lineal ni rígido. Sin embargo, trabajar con un esqueleto metodológico explícito reduce omisiones y decisiones implícitas. El flujo que se presenta a continuación no es obligatorio, pero sí razonable en la mayoría de contextos aplicados.

Este proceso general incluye:

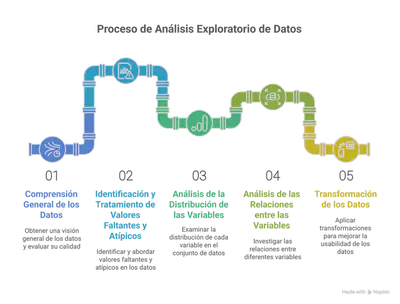
A continuación, se desarrolla cada etapa con ejemplos prácticos utilizando el paquete dlookr en R.

1. Comprensión General de los Datos y Evaluación de su Calidad

El primer objetivo del EDA no es analizar, sino orientarse. Antes de cualquier inferencia, conviene responder preguntas básicas:

• ¿Qué tamaño tiene el dataset?

• ¿Qué representa cada variable?

• ¿Los tipos de datos son coherentes con su significado?

• ¿Existen señales evidentes de problemas estructurales?

En esta etapa se revisan:

• dimensiones del dataset,

• tipos de variables,

• valores ausentes,

• rangos imposibles o sospechosos,

• estadísticas descriptivas elementales.

La función diagnose() de dlookr permite una inspección sistemática inicial:

# Para obtener un resumen rápido de las características de los datos
diagnose(mtcars_na)

El objetivo aquí no es corregir nada todavía, sino formular hipótesis informadas sobre la calidad de los datos.

2. Identificación y Tratamiento de Valores Faltantes y Atípicos

Los valores faltantes y los valores atípicos no son errores por definición. Son señales que requieren interpretación.

Valores faltantes

Antes de imputar o eliminar, es esencial preguntarse:

¿Cuántos faltantes hay?

¿Dónde se concentran?

¿Son plausiblemente aleatorios?

# Visualizar la distribución de valores faltantes
plot_na(mtcars_na)

# # Identificar valores atípicos para una variable específica (ej. "hp")
# # plot_outlier() es excelente para visualizar.
# plot_outlier(mtcars_df, "hp")

El tratamiento puede incluir:

• eliminación (cuando el impacto es marginal o la variable es inviable),

• imputación simple,

• o métodos basados en modelos.

La elección no es técnica solamente, sino contextual.

Valores atípicos

Un valor extremo puede ser:

• un error,

• una observación rara pero válida,

• o una señal de un subproceso distinto.

Las opciones clásicas (eliminar, transformar, limitar o conservar) no son intercambiables y dependen del objetivo analítico.

plot_outlier(mtcars_df, "hp")

Eliminar un outlier sin justificarlo es tan problemático como conservarlo sin examinarlo.

3. Análisis de la Distribución de las Variables

Comprender la distribución de cada variable individualmente es clave para seleccionar los métodos estadísticos y de modelado adecuados.

Variables Numéricas:

El análisis univariado permite evaluar qué supuestos son razonables y cuáles no.

Para variables numéricas:

• histogramas y densidades ofrecen información visual,

• medidas de asimetría y curtosis cuantifican la forma,

• las pruebas de normalidad pueden complementar, pero no reemplazan el juicio analítico, especialmente en muestras grandes.

plot_hist(mtcars_df, "mpg")
plot_normality(mtcars_df, "mpg"))

Para variables categóricas, las frecuencias y proporciones revelan desequilibrios que pueden condicionar análisis posteriores.

4. Análisis de las Relaciones entre las Variables

Explorar relaciones no implica afirmar causalidad. Implica detectar dependencias que merecen explicación.

Numérica vs numérica:

• gráficos de dispersión,

• correlaciones (interpretadas con cautela).

Numérica vs categórica:

• boxplots,

• comparaciones de distribuciones.

Categórica vs categórica:

• tablas de contingencia,

• pruebas de independencia.

plot_cor(mtcars_df)
plot_eda(mtcars_df, target = "mpg", feature = "wt")
plot_eda(mtcars_df, target = "mpg", feature = "cyl")

Una correlación alta es una invitación a pensar, no una conclusión.

5. Transformación de los Datos

Transformar datos no es “mejorarlos”, sino adaptarlos a un propósito específico.

• Transformaciones para asimetría.

• Escalado para algoritmos sensibles a magnitud.

• Codificación para variables categóricas.

• Ingeniería de características como acto creativo y peligroso.

mtcars_transformed_log <- transform_df(mtcars_df, mpg = log(mpg))
plot_normality(mtcars_df, "mpg")
plot_normality(mtcars_transformed_log, "mpg")

La ingeniería de características suele tener gran impacto, pero también introduce riesgos de sobreajuste y fuga de información, que deben evaluarse explícitamente.

Herramientas Populares para EDA

Para realizar un EDA efectivo, contamos con potentes herramientas en lenguajes como R y Python:

• En R:
  • El ecosistema tidyverse (dplyr para manipulación, ggplot2 para visualización) es indispensable.
  • Paquetes específicos para EDA como dlookr, es excelente por su enfoque estructurado en el diagnóstico de calidad, exploración y transformación de datos, ofreciendo funciones y reportes automatizados que agilizan el proceso.
  • Otros paquetes útiles incluyen DataExplorer, skimr, y visdat.
• En Python:
  • pandas para manipulación de datos.
  • matplotlib y seaborn para visualización estática.
  • plotly para visualizaciones interactivas.
  • Bibliotecas como missingno para visualizar valores faltantes, pandas_profiling para informes automáticos de EDA, y sweetviz para comparaciones.

Conclusión

El EDA no garantiza conclusiones correctas, pero reduce drásticamente las conclusiones ingenuas. Es el espacio donde el analista deja de ejecutar recetas y empieza a razonar con datos reales.

Dominar el EDA no consiste en memorizar gráficos, sino en aprender a formular mejores preguntas antes de modelar. Esa habilidad es la que separa el análisis técnico del análisis científico.

Pregunta para el lector

¿En qué momento de tu trabajo analítico has descubierto que el problema no estaba en el modelo, sino en lo que asumiste sobre los datos antes de modelar?

Comparte el ejemplo o la duda. El EDA no se perfecciona en silencio, sino confrontando decisiones reales.