Las trampas de la correlación disfrazada de causalidad

Por Maicel Monzon
Introducción
El ojo humano está entrenado para detectar patrones.
Cuando dos fenómenos se mueven juntos, tendemos a asumir que uno provoca al otro.
La estadística, mal interpretada, refuerza esa intuición peligrosa.
La correlación describe coexistencia; no establece causalidad.
Sin embargo, titulares, políticas públicas y decisiones clínicas se apoyan a menudo en esta confusión.
Este artículo no busca ridiculizar errores obvios, sino mostrar cómo incluso análisis técnicamente correctos pueden sostener conclusiones falsas si el razonamiento causal es débil.
1) Correlaciones llamativas (y por qué engañan)
Algunas correlaciones resultan tan evidentes que parecen absurdas. Precisamente por eso son útiles como punto de partida.
- Helados y ahogamientos. Ambos aumentan en verano. El factor común es el calor, no el helado.
- Cigüeñas y natalidad. En zonas rurales europeas, ambas son más frecuentes. La explicación está en el contexto demográfico, no en las aves.
- Películas de Nicolas Cage y ahogamientos en piscinas. Ejemplo clásico de correlaciones espurias recopiladas por Tyler Vigen.
Estos casos no son interesantes por sí mismos, sino porque revelan un mecanismo general:
una tercera variable no observada puede generar asociaciones engañosas.
2) Cuando la confusión tiene consecuencias reales
En investigación en salud, confundir correlación con causalidad no es anecdótico.
Ejemplo en política pública:
Países con mayor densidad de médicos reportan más diagnósticos de cáncer.
Conclusión errónea: “los médicos causan cáncer”.
Realidad: mayor acceso sanitario implica mejor detección.
Causalidad inversa (no bidireccional)
Un error frecuente es invertir el sentido de la relación:
Niños con bajo rendimiento escolar pasan más horas frente a la televisión.
La pregunta relevante no es retórica:
- ¿La televisión empeora el rendimiento?
- ¿O los niños con dificultades académicas recurren más a ella?
Aquí no hablamos de retroalimentación compleja, sino de una inversión plausible del sentido causal.
¿Qué es una variable de confusión?
Una variable de confusión es una tercera variable que:
- Está asociada con la exposición
- Está asociada con el desenlace
- No forma parte del mecanismo causal entre ambos
Su efecto es generar una asociación aparente o distorsionar una real.
Ejemplo: la edad puede confundir la relación entre consumo de medicamentos y mortalidad.
3) Qué mide realmente la correlación
El coeficiente de correlación de Pearson (r) mide la intensidad y dirección de una relación lineal entre dos variables continuas.
- r = +1 → relación positiva perfecta
- r = −1 → relación negativa perfecta
- r ≈ 0 → ausencia de relación lineal
Puede deberse a confusión, azar o causalidad inversa.
Un coeficiente cercano a cero no descarta relaciones no lineales.
La correlación es descriptiva. No responde preguntas causales.
4) Elegir el coeficiente adecuado no salva una mala pregunta
Existen múltiples coeficientes de correlación porque los datos y las relaciones varían.
Elegir el coeficiente correcto evita errores técnicos, pero no convierte una asociación en causal.
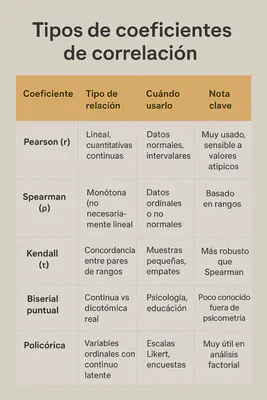
El problema central no suele ser el coeficiente, sino la interpretación posterior.
5) Causalidad: un problema de razonamiento, no de software
Establecer causalidad exige diseño, contexto y juicio crítico.
Una guía clásica son los criterios de Bradford Hill, propuestos en 1965.
Los criterios de Bradford Hill
| Criterio | Pregunta clave |
|---|---|
| Fuerza | ¿Qué tan grande es la asociación? |
| Consistencia | ¿Se replica en distintos contextos? |
| Especificidad | ¿La exposición produce un efecto concreto? |
| Temporalidad | ¿La causa precede al efecto? (obligatorio) |
| Gradiente | ¿Existe relación dosis–respuesta? |
| Plausibilidad | ¿Tiene sentido biológico? |
| Coherencia | ¿Contradice el conocimiento previo? |
| Evidencia experimental | ¿Hay respaldo experimental? |
| Analogía | ¿Existen fenómenos similares conocidos? |
Sirven para estructurar el razonamiento, no para automatizar conclusiones.
Diagramas causales (DAGs): pensar antes de ajustar
Los diagramas causales dirigidos (DAGs) permiten representar hipótesis causales antes del análisis.
Ejemplo conceptual:
El tabaquismo aumenta el consumo de café y el riesgo cardiovascular.
Si no se ajusta por tabaquismo, el café parecerá causalmente dañino.
El DAG no “demuestra” nada.
Obliga a explicitar supuestos.
6) Cuando una correlación sí condujo a causalidad
En los años 50, los estudios de Doll y Hill mostraron una fuerte asociación entre tabaco y cáncer de pulmón.
La objeción fue conocida: “correlación no es causalidad”.
La diferencia fue el razonamiento acumulativo:
- efectos grandes
- temporalidad clara
- dosis–respuesta
- plausibilidad biológica
- consistencia internacional
Aquí, la frase correcta no era descartar la correlación, sino investigarla con rigor.
7) Una metáfora útil
Ver dos hojas caer juntas no implica que una arrastre a la otra.
Ignorar el viento es ignorar la causa común.
8) Checklist mínimo de rigor causal
Antes de afirmar causalidad, pregúntate:
- ¿Existe una variable no considerada que explique la asociación?
- ¿El efecto podría preceder a la supuesta causa?
- ¿El diseño permite inferencia causal o solo asociación?
- ¿El tamaño del efecto es clínicamente relevante?
- ¿La conclusión depende de supuestos no explicitados?
Si no puedes responderlas, la correlación no basta.
9) P-hacking: correlaciones fabricadas
El p-hacking consiste en explorar múltiples análisis hasta encontrar un resultado “significativo”.
Con suficientes pruebas, el azar garantiza falsos positivos.
Señales de alerta:
- muchas variables, pocas hipótesis previas
- resultados sorprendentes sin plausibilidad
- ausencia de preregistro
- efectos pequeños presentados como hallazgos mayores
Solo indica compatibilidad estadística bajo supuestos específicos.
Conclusión
La correlación es un punto de partida, no una conclusión.
Sin razonamiento causal explícito, incluso análisis impecables pueden inducir a error.
La próxima vez que leas que “X causa Y”, haz una pausa crítica.
La estadística describe. El pensamiento decide.
Para cerrar (y abrir la conversación)
Si trabajas con datos reales —en salud, investigación o políticas públicas—, es muy probable que ya te hayas enfrentado a una correlación tentadora.
La pregunta no es si existe una correlación, sino si te atreviste a interrogarla.
👉 Pregunta para la caja de comentarios:
¿Has visto alguna vez una decisión importante (clínica, regulatoria o científica) apoyarse en una correlación que no resistía un análisis causal serio?
¿Dónde falló el razonamiento: en el diseño, en el análisis o en la interpretación?
Si quieres, descríbelo de forma general (sin datos sensibles). Responderé señalando qué tipo de trampa causal está en juego y cómo habría que replantearla.
“Si te gusta cuestionar los datos y la IA con rigor, suscríbete a mi boletín en LinkedIn para no perderte estos análisis semanalmente.”
¿Te interesa pensar más allá de los números?
Suscribirse al Boletín en LinkedInBibliografía
Hill, A. B. (1965). The environment and disease: association or causation?
Hernán, M. A., & Robins, J. M. (2020). Causal Inference: What If.
Pearl, J. (2009). Causality.
Silva Aycaguer, L. C. (1998). Cultura estadística e investigación científica.
Vigen, T. (2015). Spurious Correlations.